シュレーディンガー方程式は量子力学において基本となる方程式ですが、そもそも波動関数が何なのかというところでつまずくのが普通です。 ド・ブロイ波を表す波動関数 $Ψ$ とはどのような形なのか、なぜそこに虚数が出てくるのか、その関数が持つ意味は何なのでしょうか。

虚数という道具

量子力学でよく目に留まるのが虚数 $i$ です。 虚数が出てくる時点で異世界か何かを想像してしまう人がいるかもしれませんがそれは完全に誤解です。 虚数は波や振動を表現する道具として、電気工学などの分野では日常的に使われています。

まずは波の式を普通に書いてみます。 $u$ を縦軸、$x$ を横軸に取り、$t$ を時間とすると、波が動いていく様子がグラフに現れます。

　　$u = cos(ax-bt)$

数学のオイラーの公式によれば、$cos$ 関数は次のように書き換えることもできます。 $u$ は複素数になり、虚数の波（黄線）も余分に出てくるのですが、$u$ の実数部（青線）だけに着目すればどちらもまったく同じ波形になります。 どちらの式を使うかはお好み次第というわけです。

　　$u = e^{i(ax-bt)}$

さてここでついでに出てきた虚数の波ですが、必ず元の波と１／４波長だけずれているという特徴があります。 数学上ただそれだけのものでしかないのですが、この特徴を使えばまどろっこしい計算式や方程式がわりと簡潔に表現できる場面があるのです。 波を複素数で表し、架空の波を使って式をシンプルにまとめる。 これは数学上のテクニックです。

ド・ブロイ波の振動数

ド・ブロイによると運動量 $p$、エネルギー $E$ の粒子は振動数と波長を持った波としてふるまいます。

　　$\displaystyle ν = \frac{E}{h}$
　　$\displaystyle λ = \frac{h}{p}$

単純に考えればド・ブロイ波は次の関数で表せるはずです。 これが振動数 $E/h$、波長 $h/p$ の波であることはグラフを書いてみれば確認できます。

　　$\displaystyle Ψ = cos(\frac{2π}{h}(px-Et))$

ところでこのエネルギー $E$ とは何のエネルギーでしょうか。 運動エネルギーと位置エネルギーのことでしょうか、 それとも相対性理論から導かれる $mc^2$ の静止エネルギーも含んだものでしょうか。 それはどちらで計算しても構いません。 結果的にはどちらでもつじつまが合うからです。

・・・ちょっと待ってください。 エネルギーをどう考えるかによってド・ブロイ波の振動数が変わってしまいます。 それで構わないとすれば、そもそもその振動には何の意味があるのでしょうか。

波動関数は何を表すか

波の関数が表すものは何でしょうか。 水の波であれば水面の高さのゆらぎを表しています。 音波であれば空気の密度のゆらぎを表しています。 ではド・ブロイ波の関数 $Ψ$ とは一体何を表しているのでしょうか。

結論としてド・ブロイ波の関数そのものは物理的な何かを表しているわけではありません。 あくまで仮想的な計算上の道具です。 振動数はどうであろうと構いません、実際に何かが揺れているわけでもないでしょう。 ただその仮想的な波の振幅（振れ幅）には物理的な意味があります。

ド・ブロイ波は本当の波のように干渉し、場所によって振幅が大きくなったり小さくなったりしています。 そしてその波は捕まえようとすれば粒子に姿を変えてしまいます。 このとき、波の振幅が大きな場所では粒子が見つかりやすく、 波の振幅が小さな場所では粒子が見つかりにくいのです。

波動関数のグラフ

粒子の位置が不確定なのは二重スリット実験のときだけではありません。 真空中をただまっすぐに飛んでいる粒子もまた波としてふるまっており、粒子の位置は不確定性を伴います。 ただ波動関数の振幅が大きいところで粒子は見つかりやすいはずです。 もう一度波動関数を見てみましょう。

　　$\displaystyle Ψ = cos(\frac{2π}{h}(px-Et))$

そういえば $cos$ 関数の振幅なんてどこでも一定です。 これでは粒子が見つかりやすい場所も見つかりにくい場所もなく、どこにあるのかまったく見当がつかないのではないでしょうか。 もちろんこの結論はおかしい。 原子の位置が完全に不確定なら我々は物体を視認することも触ることもできないはずです。

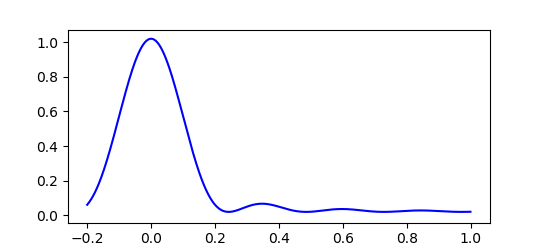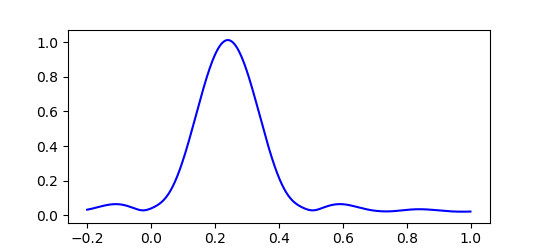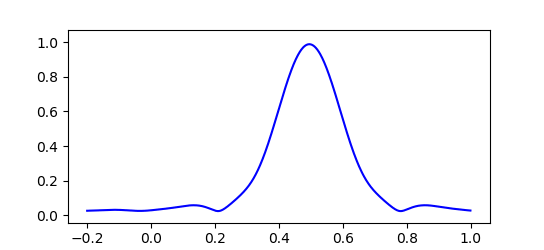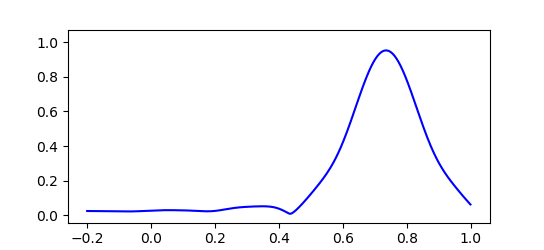
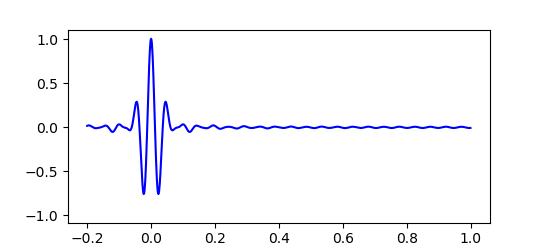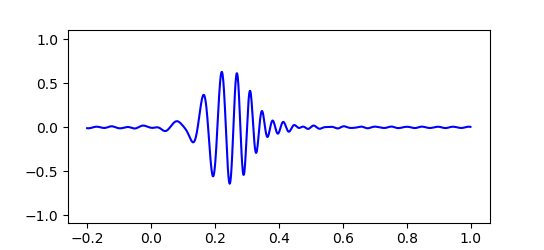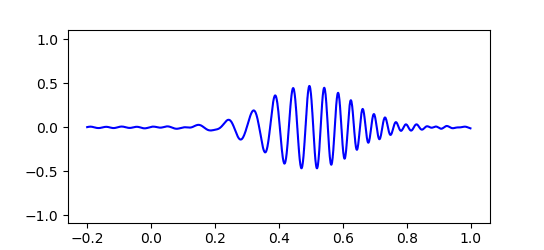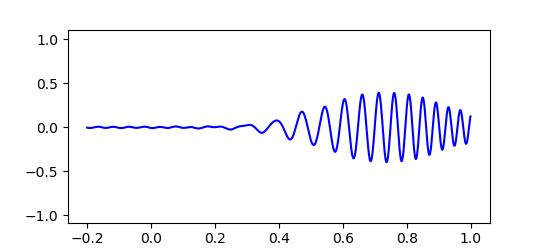
実際のところド・ブロイ波はこのような単純な $cos$ 関数一つだけで表されるものではありません。 粒子の運動量 $p$ やエネルギー $E$ にもわずかな不確定性があり、ド・ブロイ波は波長や振動数がわずかにずれた波が重なり合った状態で存在しています。 すると下図のように波の大部分は打ち消しあい、振幅が大きくなる場所はある程度限られてきます。 このため粒子はいつもだいたい限られた範囲で見つかるのです。

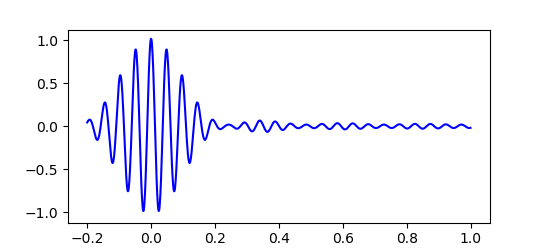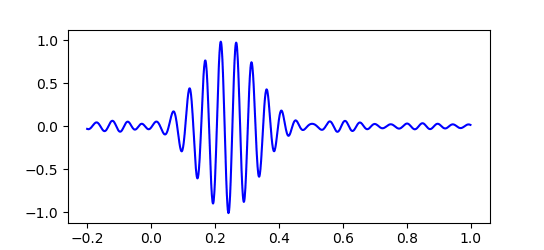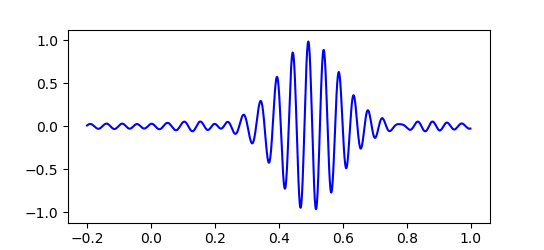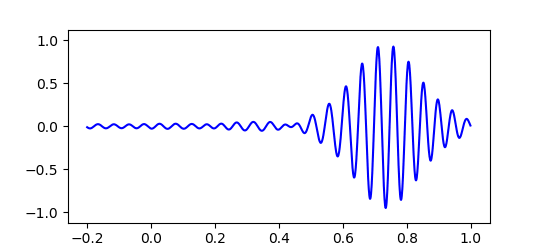
位置と運動量の不確定性

最初にド・ブロイ波の波束を狭くしてみると、その後すぐに波束は広がってしまい位置が不正確になっていきます。 粒子の位置を正確に特定するほど運動量は不正確になり、次に粒子の位置を調べたときあらぬところで見つかる可能性があることを示しています。

逆に粒子の運動量が正確に決まっているならば、その粒子はどこにあるのか誰にもわからないはずです。 運動量を変えたくなければ位置を調べてはいけません。 位置のヒントが得られてしまうような測定方法を試みれば、その行為によって運動量はまた不確定な状態になってしまうからです。

位置と運動量を同時に正確に知ることはいかなる手段でもうまくいきません。 これが量子の世界の奇妙なところです。

波の振幅の求め方

波動関数のグラフで本当に知りたいのはその振れ幅（振幅）です。 グラフの形をみればなんとなくわかるものですが、微妙な揺れ方をしている部分もあり明確にはわかりにくいのではないでしょうか。 そこで便利な道具として登場するのが最初に述べた波の複素数表現です。

複素数で表現された波には次の公式が使えます。 これは量子力学に限った計算式ではなく、一般的な波の振幅を数学的に求ることができます。

　　$|Ψ|^2 = Ψ^*$ $Ψ$

この公式を利用し、先ほどの波動関数の振幅をグラフにしたものがこれです。 グラフの縦軸は波の振幅 $|Ψ|$ を表しています。 最初の幅がシャープな波ほどすぐに崩れていくのがわかります。