これまで日常的な現象のほとんどはニュートン力学で正確に説明できていたといってよいでしょう。 しかしそこからさらに宇宙に目を向け、光に近い速度を扱おうとするならば相対性理論の効果を計算に入れなければなりません。

今回はこれまでニュートン力学で扱ってきた、運動量、エネルギー、力が相対性理論によってどのような修正を受けるのかを具体的に見ていきます。

運動量

力学には「運動量保存の法則」という重要な法則があります。 物体どうしがどのように力を及ぼし合おうとも運動量の合計は変わらないことが保証されています。

ニュートン力学での運動量は $ $$p=mv$ でしたが、光速に近い速度では誤差が出ます。 相対性理論の効果を考慮した場合、運動量は $p=γmv$ となります。

この $γ$ は以前にも出てきたローレンツ因子です。

　　$\displaystyle γ = \frac{1}{\sqrt{\displaystyle 1-\frac{v^2}{c^2}}}$

速度が遅ければほぼ $γ=1$ になるため、従来の運動量との違いはごくわずかです。 光速に近い運動を扱うのでなければ、今までどおり $p=mv$ で計算して差し支えありません。

運動エネルギー

エネルギーについても保存則があります。 ニュートン力学での運動エネルギーは $\displaystyle K=\frac{1}{2}mv^2$ でしたが、 これについても光速に近い速度では誤差が出るため修正を加えなければなりません。 相対性理論の効果を考慮した運動エネルギーは次の式になります。

これも速度が遅ければ計算結果はニュートン力学とほぼ変わりません。 光速に近い運動を扱うのでなければ、今までどおり $\displaystyle K=\frac{1}{2}mv^2$ で計算して差し支えないでしょう。

力

力については「作用反作用の法則」があります。 物体が力を及ぼし合うとき、必ずお互い逆向きに同じ大きさの力が働いているはずです。

ニュートン力学で力は $F=ma$ で表されますが、 この式を変形すれば $\displaystyle F=\frac{Δp}{Δt}$ という関係も成り立ちます。 どちらでも同じなのでどちらを使ってもよかった。 しかし相対性理論ではこの２つの値は一致しません。

相対性理論において $F = ma$ という定義は作用反作用の法則が成り立たない意味がないものになります。 力の定義は $\displaystyle F=\frac{Δp}{Δt}$ でなければいけません。 力とは運動量を変化させるものだと考えれば、作用反作用の法則が成り立ち、運動量保存の法則を説明できる意味のある物理量になります。

運動量と運動エネルギーの考察

ちなみに相対性理論では運動量がなぜ $p=γmv$ になるとわかったのでしょうか。 相対性理論の発表当時、実験によりこの関係式を見つけ出したわけではありません。

次のように２つの球の弾性衝突を考えてみましょう。 ２つの球は必ず運動量保存法則が成り立つように跳ね返るはず。 衝突前後で運動量の合計は変わらないはずです。

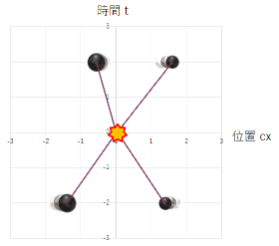
この運動量保存の法則は別の慣性系で見ても成り立っていなければなりません。 ローレンツ変換により慣性系を変えて見てみます。

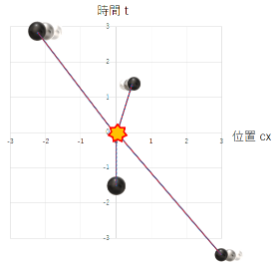
実際に数値をあてはめて計算してみると $p=mv$ で計算しても結果が合わないはずです。 どの慣性系で見ても運動量保存の法則が成り立つのは運動量を $p=γmv$ とした場合だけ。 つまり運動量は $p=γmv$ であるはずです。

速度と運動量の関係がわかれば必然的に速度と運動エネルギーの関係もわかります。 速度 $0$ から $v$ まで加速するのにどれだけの仕事が必要かを考えればよいのです。 運動エネルギーは物体にした仕事 $F・Δx$ の分だけ増えるはず。 そこから運動エネルギーは $K=γmc^2-mc^2$ であることが導かれます。

光速を超えられない

物体に力を加え続ければ運動量は際限なく増えていきます。 しかしどれだけ運動量が増えても速度が光速を超えることはありません。 それは $p=γmv$ を速さについて解いてみればわかります。

　　$\displaystyle v = c \sqrt{\frac{p^2}{m^2c^2+p^2}}$

運動量 $p$ が増えれば増えるほど速度の上がり方がゆるやかになり、どこまでいっても物体の速度 $v$ は光速 $c$ 以上にならないことを示しています。

運動量保存則が成り立たない？

先ほど運動量の考察では物体の弾性衝突について考えました。 しかし非弾性衝突の場合で計算してみると運動量の計算が合わない、つまり運動量保存の法則が成り立っていないように見えます。

弾性衝突と非弾性衝突では何が違うのか。 非弾性衝突では物体の運動エネルギーの一部が別の形に変わります。 熱エネルギーとなり物体の温度を上げるか、もしくは音や光としてどこかに飛んで行くかです。

衝突時に音や光が外に出て行ってしまえば運動量が失われるのは当然なので、何も出て行かず物体の温度が上がる場合を考えてみます。 このとき運動量の計算が合わないのはどうしてでしょうか。

質量とエネルギーの等価性

一つ見過ごしているのは、熱運動しているひとつひとつの分子にも相対性理論の効果が及んでいるということです。 物体内部の分子ひとつひとつがばらばらの方向に運動量 $p=γmv$ で動いていれば、 物体全体はまるで平均質量が 「$γm$」 であるかのように加減速しにくくなるはずです。

そして運動エネルギー $K=γmc^2-mc^2$ は、 物体のみかけの質量「$γm$」が $1$ キログラム増えたとき分子の運動エネルギーは $c^2$ ジュール増えているという関係を示しています。

ここからアインシュタインは思いもよらない発想をします。 運動エネルギーが質量のように見えるということはその他の内部エネルギーも質量のように見えるのではないか。 そもそも我々が質量と呼んでいるものは、物体のエネルギーによってもたらされている性質に過ぎないのではないかと。

アインシュタインは質量とエネルギーは同じものだと考えたのです。 つまり質量 $m$ の物体は静止していても $mc^2$ という莫大な内部エネルギーを持っていることになります。

この考えが正しければ、先ほどの非弾性衝突により運動量が失われてしまうように見える問題は解決します。

衝突前後で運動エネルギーと内部エネルギーの合計 $E = γmc^2$ は変わっていないはずです。 衝突で失われた運動エネルギーは熱エネルギーやその他の内部エネルギーに変わっており、 物体の質量 $m$ は少し増えているはず。 この質量の増加を計算に入れれば、運動量保存の法則は完全に成り立つことになります。