座標変換
物事は様々な捉え方ができることを意識しておかなければなりません。 事実は一つでも観点は人それぞれ違います。 他人は物事のまったく別の側面を見ているかもしれません。 捉え方が人によって違うのは当然なのです。
座標系とは
座標系の考え方はガリレオの時代まで遡ります。 1637年にルネ・デカルトは平面に格子状の線を引き、数値の組み合わせで位置を表現するという方法を確立します。 この座標という表現方法がなければ物理学で語れることはほとんど何もなかったでしょう。
この格子線や数値は人が頭の中に思い浮かべたものに過ぎません。 どこを中心に線を引くか景色をどちらから眺めるか誰も決めなければ、 格子線の引き方や割り当てる数値は人それぞれです。
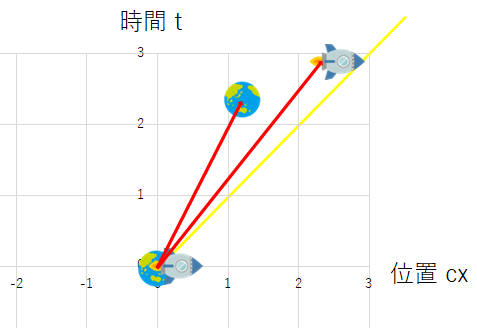
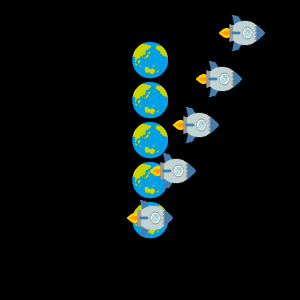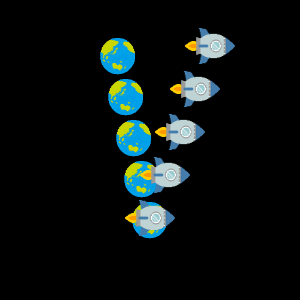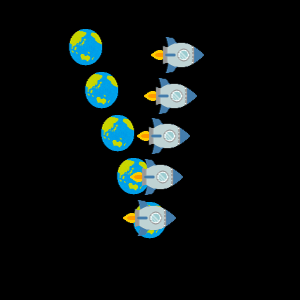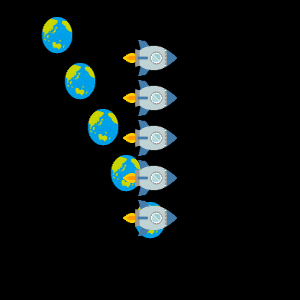
縦軸に時間座標、横軸に位置座標を記載した図もお馴染みのものかと思います。 次の図は時刻 $ $$t=0$ に飛び立ったロケットが地球から離れていく様子を表しています。

これをロケットを中心に考えてみれば、動いているのは地球の方です。 まったく同じ出来事も少し頭を切り替えてみれば、次のような座標系を思い浮かべることができます。

この2つの図はどちらもまったく同じ出来事を表しています。 ただ座標の取り方によって、同じものを見ているのに座標の値は変わってしまうのです。
同じ出来事に対して人それぞれどういう座標系を思い浮かべていようが構いません。 しかしこれで困るのはお互いに話をするとき話が噛み合わないことです。 思い浮かべている座標系が違うならどちらかがどちらかに合わせてやらなければなりません。 それを行うのが座標変換です。
ガリレイ変換
上側の図の地球とロケットを次の数式に従って動かしてみてください。 $v=0.5$ でガリレイ変換すると、先ほどの下側の図と同じになることがわかります。
$x = x - vt$
$t = t$

もちろん座標変換で実際の地球やロケットが動くわけではありません。 座標系とはいわば頭の中の地図です。 座標変換とはアプリの地図画面をスクロールしたり回転させるのと同じことです。
ローレンツ変換
ところが現実にはガリレイ変換のとおりになりません。 光の速さに近くなるとガリレイ変換との誤差が目立ってきます。 ローレンツは次の変換式が成り立つと述べています。
$x = γ(x - vt)$
$\displaystyle t = γ(t - \frac{vx}{c^2})$
この $γ$ はローレンツ因子と呼ばれるもので次の値になります。
$\displaystyle γ = \frac{1}{\sqrt{\displaystyle 1-\frac{v^2}{c^2}}}$
先ほどのように $v$ の値を少しずつ変えたアニメーションがこちらです。 ご覧のとおり、ローレンツ変換ではあらゆる出来事の時間座標も変化します。
ミンコフスキー時空
1908年ミンコフスキーは、この世界でどのような幾何学が成り立っているのかを考察します。
我々は普段この世界を3次元の空間だと考えています。 相対性理論の発見以前の科学者たちもそうでした。 しかし現実に我々が時間と呼んでいるもの、そして長さと呼んでいるものは測り方によって変わってしまう。 これはこの世界が3次元の空間という前提が間違っていることを意味します。 この世界は4次元の時空間「ミンコフスキー時空」と考えられるのです。
ミンコフスキー時空の中では何が起こるか見ていきましょう。 次の図は地球側の視点を表しています。 今回はx軸の1目盛りの長さを $c$ メートルとしてグラフを書いています。
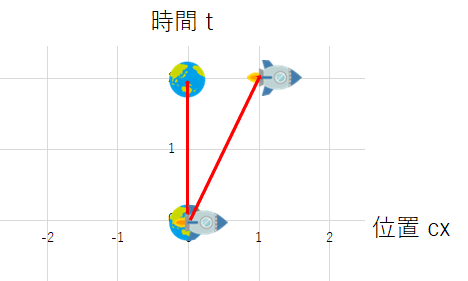
さてこの状況をロケットを基準に考えてみます。

2つの図は捉え方が違うだけでまったく同じ出来事を表しています。 地球側の視点では同時とみなせる出来事が、ロケット側の視点では同時ではなくなっています。 我々が住むこの世界の時間は万人に共通のものではないのです。
速度の合成則
速度は時空図上の傾きで表されます。 光の軌道は常に斜め45°の線で表され、これはローレンツ変換しても変わりません。 そして光速未満で動く物体の軌道はどのようにローレンツ変換しても光速に達することはありません。 つまり物体の速度は誰から見ても光速以上にはなりえないということです。
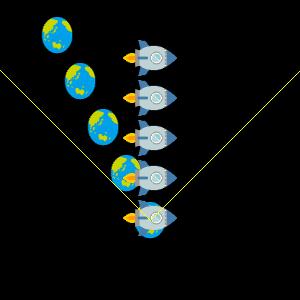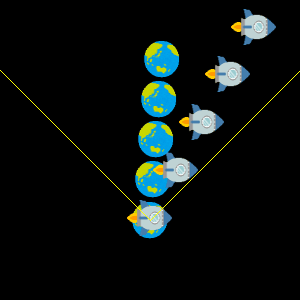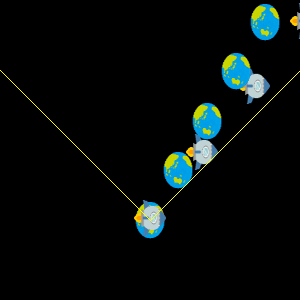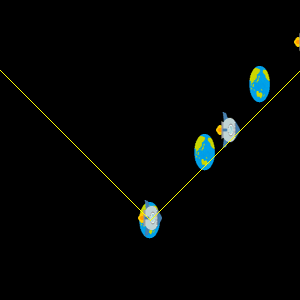
私たちが日常使っている相対速度の計算 $v=v_A+v_B$ は、光速に近くなると通用しません。 相対性理論の効果を考慮すると次の式になります。
$\displaystyle v = \frac{v_A+v_B}{\displaystyle 1+\frac{v_Av_B}{c^2}}$
光速未満の速度をどんなに足し合わせても光速に達することはありません。 どんなに追いかけても決して光に追いつくことはできないのです。