

ファラデーは実験とそれに基づく直観に優れた科学者でした。 ファラデーの研究結果は数学を使っていないものの、 場の概念や力線という考え方などその研究手法は実に数学的であると感じたマクスウェルは、 電磁気の諸現象について数学的な統一という考えを持つようになります。
1864年マクスウェルは、電磁気学の場に関する次の4つの法則をベクトル解析を用いた数学的な表現に書き直しました。
・ガウスの法則
・ファラデーの電磁誘導の法則
・単独の磁極は存在しない
・アンペールの法則
これが電磁気学の分野で基礎となる非常に重要な4つの方程式。 マクスウェル方程式です。
$E$ が電場、$H$ が磁場 、$D$ が電束密度、$B$ が磁束密度、$t$ は時間、$i$ は電流、$ρ$ は電荷密度です。 式を一つずつ見ていきましょう。
ガウスの法則を簡単にいえば、 空間をどんな形に囲っても、そこから出ていく電束の数と、その内側にある電荷の合計は必ず一致するという法則です。
例えば下の図で緑色の曲線から出入りする電束の数は差し引き±0です。 これ以外にも好きな部分を曲線で囲ってみてください。 +電荷だけ囲った場合は曲線から出ていく電束の方が13本多く、−電荷だけ囲った場合は曲線に入ってくる電束の方が13本多く、両方囲った場合は±0本となるはずです。 つまりは、この図に書かれている電荷は +13クーロンと -13クーロンだということが読み取れます。
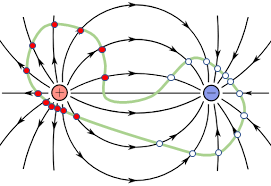
マクスウェル-ガウスの式は数学的にこれと同じことを表現しています。 電束は電荷のないところで湧き出したり消えたりせず、 正電荷から湧き出し、負電荷で消失することを意味します。
div $D = ρ$
ファラデーは、コイルを貫く磁束密度に変化があったときコイルに起電力が発生することを発見しました。 それを表現したのがこの式です。 ある場所で磁束密度が変化すれば、その周囲を回るように電場が発生するということを意味しています。
rot $\displaystyle E = -\frac{∂B}{∂t}$
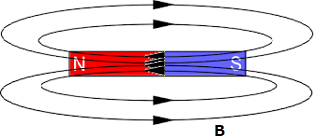
磁石には必ずN極とS極があります。 真ん中で切ってもN極とS極を分けることはできず、切り口に新たなS極とN極が現れます。 それを説明したのがこの式です。
この式が正しいなら、磁束はどこにも切れ目のないひとつづきの輪になっています。 磁石がどんな形であろうが、出ていく磁束と入ってくる磁束は必ず同数となり、 決してN極だけの磁石やS極だけの磁石は存在しないことになります。
div $B = 0$
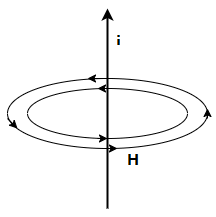
アンペールの法則は、rot $H = i$ で表すことができます。 導線に電流が流れていれば、その周囲を回るように磁場が現れることを意味しています。
しかしこの式には一つの問題がありました。 静電気の放電や、積乱雲からの落雷のように、ある場所からある場所に一瞬だけ電流が流れる現象を考えたとき、 この式が成り立つはずがないのは数学的に明らかなのです。
アンペールの法則を書き直すのはあきらめるしかないのでしょうか。 いえ、そもそもアンペールやビオ・サバールは定常電流で成り立つ法則を調べたに過ぎません。 アンペールの法則やビオ・サバールの法則こそまだ何かが足りていない可能性があります。
マクスウェルは他の3つの式との対称性を考え、正確には次の式が成り立つはずだと考えました。 これで4つ目のマクスウェル方程式の完成です。
rot $\displaystyle H = i + \frac{∂D}{∂t}$
マクスウェルはこの4つの方程式が正しければ「電磁波」という現象が存在するはずだと予言しました。
方程式をもう少し簡単に、近くに電荷も電流も物質も何もない真空中ではどうなるかを考えます。 $ρ = 0$、$i = 0$、 真空中なら $E = D/ε_0$ なので電場 $E$ に統一します。 同じく磁場も $B = μ_0H$ に統一し、 マクスウェル方程式は次のように変形することができます。
div $E = 0$
rot $\displaystyle E = -\frac{∂B}{∂t}$
div $B = 0$
rot $\displaystyle B = μ_0 ε_0 \frac{∂E}{∂t}$
これで $B$ と $E$ の関係が少しだけ見えてきます。 $B$ が変動することによって $E$ が変動し、 $E$ が変動することによって $B$ が変動するというように、 お互いがお互いを変動させ続ける可能性があることを想像できます。
マクスウェルはこの方程式を解き、電場と磁場はお互い直角に横波として空間を伝わっていくはずだという結論を導きます。 その速さは $1/\sqrt{μ_0 ε_0}$ で、なんと光の速さと同じ秒速30万kmとなる計算です。
1871年マクスウェルはこの「電磁波」こそが光の正体なのだと説きます。 電磁波の速さが光の速さと一致しているのは偶然ではないと考えたのです。