

エントロピーの法則では、物体の変化が時間の経過とともにどのように進むかがわかります。 しかしこれが少し不思議なのです。 もともとニュートンの運動方程式には時間反転対称性があります。 つまり粒子の運動を録画し、それを巻き戻しで見たとしてもまったく違和感がない運動になるはずです。
しかしエントロピーの法則では時間反転対称性が破れており、マクロなスケールで物事を見れば時間の方向ははっきり区別できます。 つまりエントロピーはニュートン力学から出てくるようなものではないのです。
1860年マクスウェルは、気体分子の速度に関してマクスウェル分布を導きます。 ボルツマンはマクスウェルらに続き気体分子運動論を研究し統計力学を創始します。 そこからエントロピーの正体が見え始めます。
1877年、ボルツマンは次の関係式を導きます。
$S$ がエントロピー、$W$ がその系に存在する状態数、$\ln W$ は $W$ の自然対数を表します。 $k$ は比例定数ですが、これが何かはとりあえず後回しにします。
この式の右辺には温度も熱もエネルギーも何も入っておらず、まるで物理とは無関係な式に見えます。 本当にこれが今まで扱ってきたエントロピーと同じものなのでしょうか。 まずはこの式を紐解いていきましょう。
容器の中に1つの分子が入っているとします。 この分子の位置を問われたときどう答えればよいでしょうか。 容器の右側あるいは左側と答えるなら状態は2通りしかありません。 より詳しい位置を答えるならそれに応じて考えなければならない状態は多くなるはずです。 物事をどれだけ細かい尺度で捉えるかで状態数は変わるものです。
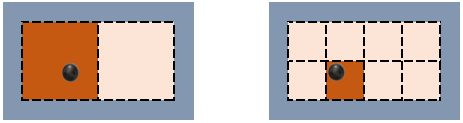
容器の体積を $V$ $[m^3]$、位置の分解能を $δ_x$ $[m]$ とすれば、考えられる状態の数は $V/δ_x^3$ と計算できます。
分子の状態とは位置だけの話ではありません。 運動量も様々でしょうし、場合によってはどのように回転しているかも考えなくてはいけません。 それらのすべての組み合わせを考えれば、たった1つの分子にも沢山の状態があることが想像できます。
簡単にするため断熱容器にヘリウムなどの単原子分子が1つだけ入っている場合で考えます。 単原子分子ならば回転運動は存在しません。 分子の速さは常に一定になるはずで、運動量ベクトルは下図の赤い升のどれかを指すことになります。 白い升を指すことはあり得ません。
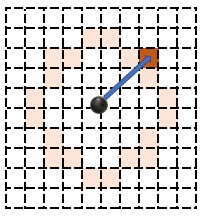
分子の運動エネルギーを $E$、分子の質量を $m$、運動量の分解能を $δ_p$ とすれば、 とりうる運動量の状態数は $8πmE/δ_p^2$ です。
容器の中に複数の分子が入っている場合はさらに複雑です。 分子の位置だけでも組み合わせは無数にあり、その位置一つ一つのに対してさらに無数の運動状態が考えられます。 すべての組み合わせを考えれば、容器の中の気体がとりうる状態数は非常に多くなります。
単原子分子から成る気体の場合、 分子数を $N$、容器の体積を $V$、内部エネルギーを $E$、分子1つの質量を $m$、位置の分解能を $δ_x$、運動量の分解能を $δ_p$ とすれば、状態数は以下の式で表せます。
$W = \displaystyle \frac{V^N}{δ_x^{3N}} \frac{3Nπ^{\frac{3N}{2}}(2mE)^{\frac{3N-1}{2}}}{\displaystyle \frac{3N}{2}!}\frac{1}{δ_p^{3N-1}}$
階乗の計算が厄介ですので、スターリングの近似公式 $n!≒\sqrt{2πn} (n/e)^n$ を利用して変形します。
$W ≒ \displaystyle \frac{V^N}{δ_x^{3N}δ_p^{3N-1}} (\frac{4πmE}{3N})^{\frac{3N-1}{2}} e^{\frac{3N}{2}}×\sqrt{2}$
式をもう少しシンプルにしたいところです。 分子数 $N$ が十分大きければ、$3N$ も $3N-1$ もほとんど同じと考えてしまってよいでしょう。 さらに $δ_x$ と $δ_p$ は掛け併せてしまって $h$ で表します。 右肩に指数もついていない $\sqrt{2}$ など掛けたところでほとんど影響がないため捨ててしまいます。 すると状態数はだいたい以下の式で近似できます。
$W ≒ (\displaystyle \frac{V}{h^3} (\frac{4πmE}{3N})^{\frac{3}{2}}e^\frac{3}{2})^N$
近似といっても誤差はそれなりにあるのですが、エントロピーに直せばほとんど誤差は目立たなくなると考えてかまいません。
$S = k\ln W$
$ ≒ kN\ln(\displaystyle \frac{V}{h^3} (\frac{4πmE}{3N})^{\frac{3}{2}}e^\frac{3}{2})$
こうして出てきたエントロピーは、クラウジウスが提唱したエントロピーとある程度似た性質を持ちます。
同じ物体を2つ合わせればエントロピーは単純に2倍になるはずです。 気体であれば容器の体積、分子数、内部エネルギーをそれぞれ2倍にしても同じことです。 しかし先ほどの式で$V,N,E$をすべて2倍にして計算してみると、エントロピーは2倍よりわずかに大きくなってしまいます。
ここでもし分子ひとつひとつが全く区別できないものと仮定すればどうなるか、この前提で状態数を数え直してみます。
$W = \displaystyle \frac{V^N}{δ_x^{3N}} \frac{3Nπ^{\frac{3N}{2}}(2mE)^{\frac{3N-1}{2}}}{\displaystyle \frac{3N}{2}!}\frac{1}{δ_p^{3N-1}} \frac{1}{N!}$
$W ≒ (\displaystyle \frac{V}{Nh^3} (\frac{4πmE}{3N})^{\frac{3}{2}}e^\frac{5}{2})^N$
$S ≒ kN\ln(\displaystyle \frac{V}{Nh^3} (\frac{4πmE}{3N})^{\frac{3}{2}}e^\frac{5}{2})$ ・・・(1)
これだと$V,N,E$をすべて2倍にしたときエントロピーはちょうど2倍になります。 なぜこの考え方でうまくいくのか不思議ですが、同じ種類の分子や原子には少しの個性もなく、 ひとつひとつ区別することができないのは確かなようです。 これについての言及は量子力学の誕生まで待つことになります。
ここで少し、ヘリウムやネオンといった単原子分子から成る気体の性質について振り返っておきます。 単原子分子理想気体の内部エネルギーは $\displaystyle U = \frac{3}{2}nRT$。 この式はモル数 $n$ の代わりに分子の個数 $N$ を使えば次のように書き直せます。
$\displaystyle E = \frac{3}{2}NkT$ ・・・(2)
$E$ は内部エネルギー、本章の書き方に合わせて記号 $E$ を使っていますが意味も単位も $U$ と同じです。 $k$ はボルツマン定数と呼ばれ、およそ $1.38×10^{-23}$ です。
さてこのボルツマン定数の $k$ 、先ほどのエントロピーの式にも同じ $k$ の記号が使われていますが、果たして関係あるのでしょうか。
一旦クラウジウスの立場からエントロピーを見直してみます。 均一に拡散された気体はエントロピーが最大化している状態と考えられます。 エネルギーの出入りがない限りはエントロピーが変わる余地はなく $ΔS = Q/T$ です。 内部エネルギー $E$ を使えば $ΔS = ΔE/T$ とも表せます。 これを微分で表せば次の式になります。 (添え字 $_V$ は容器の体積は一定とすることを明記するために付けています)
$\displaystyle {\Bigl(\frac{∂S}{∂E}\Bigr)}_V = \frac{1}{T}$
これが単原子分子の理想気体であれば(2)式より次のように変形できます。
この $k$ はボルツマン定数です。
$\displaystyle {\Bigl(\frac{∂S}{∂E}\Bigr)}_V = \frac{3}{2} \frac{kN}{E}$
一方で、ボルツマンのエントロピー(1)式を実際に $E$ で微分してみるとどうでしょう。
$\displaystyle {\Bigl(\frac{∂S}{∂E}\Bigr)}_V = \frac{3}{2} \frac{kN}{E}$
結局どちらでもまったく同じ答えに辿り着きます。 つまりボルツマン定数の $k$ と、エントロピーの係数 $k$ はまったく同じものということです。
式の中であと一つ扱いに困るのは分解能 $h$ です。 自由に決めてしまってもかまわないのですが、当然エントロピー $S$ の値は人によってまちまちな答えが出てしまうことになります。
エントロピー $S$ の値そのものに意味があるわけではなく、意味があるのはその変化量 $ΔS$ だと考えれば、人それぞれの答えで構わないのかもしれません。 しかし決めておかないとおそらく不便なことも出てくるでしょう。 決めるとすればどんな値が妥当かということです。
現在では分解能にプランク定数 $h = 6.62607015×10^{-34}$ が使われています。 なぜこの値が妥当かについては、後に熱力学第3法則そして量子力学で明らかになります。
標準状態(1気圧25℃)での1molの気体ヘリウムのエントロピーを実際に計算してみます。
計算に使う物理量は次の値になります。
$k = 1.38065×10^{-23}$ ボルツマン定数
$N = 6.02214×10^{23}$ ヘリウム分子の数
$h = 6.62607×10^{-34}$ プランク定数
$m = 6.64648×10^{-27}$ ヘリウム分子1個の質量 $[kg]$
$V = 0.0244654$ 標準状態での1molの理想気体の体積 $[m^3]$
$E = 3718.44$ 標準状態での1molの単原子分子理想気体の内部エネルギー $[J]$
これを(1)式に当てはめてエントロピーを計算すると、$S = 126.044$。 エントロピーの実測値は $S = 126.150$ です。
このわずかな誤差の原因はヘリウムを理想気体として体積、内部エネルギー、状態数を計算しているためです。 実際には分子一つ一つにも大きさがあり分子間力も働くため理想気体の理論値からわずかにずれています。
エントロピーとは物体が取り得る状態の数から計算できるもの。 つまりミクロな状態の多様性を表す尺度だということがわかりました。
物体の中で分子の運動がお互い制約され、秩序を持って動いているときは物体のエントロピーが低い状態です。 何かのはずみに制約が外れ秩序が乱れてしまえば放っておいて元に戻ることはありません。 どこかに新たな秩序を生み出そうとすれば、代わりにどこかの秩序を乱すことになります。 最終的に宇宙はすべての秩序が失われる方向に向かっていきます。 これがエントロピー増大の法則です。
宇宙のエントロピーが最大化してしまった世界は、マクロな我々にとっては静かで均一で永久に何の変化もないように見える死の世界です。 しかし個々の分子の立場で想像してみれば、その世界では何の縛りもなく、最も多様性のある自由な世界なのかもしれません。