

1824年カルノーは蒸気機関の熱効率について研究し、熱から動力を生み出すのには温度差が必要なことを発見しました。 1840年代にはマイヤー、ジュール、ヘルムホルツによってエネルギー保存則が発見されました。
1865年クラウジウスは、これらの発見から導き出される結論を熱力学の法則としてまとめます。
ここで仕事とは何かについてもう一度考え直してみます。
この宇宙にあるエネルギーの合計は変わりません。
例えば何かを持ち上げて位置エネルギーが増えたのであれば、そのぶん自分のエネルギーは失われているはずです。
要するに仕事とはエネルギーを受け渡す行為にほかなりません。

何かが仕事をしていればその一方で仕事をされているものが必ずあるはずです。 仕事をされた側のエネルギーは増えますが、そのぶんだけ仕事をした側のエネルギーは奪われているはずです。
これが熱力学第1法則、いわゆるエネルギー保存則です。
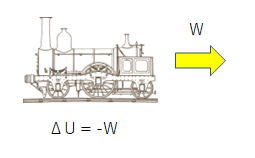
「物体のエネルギーは、物体に渡されたエネルギーのぶんだけ増え、物体が渡したエネルギーの分だけ減る」ということを式にすれば次のようになります。
$ΔU$ が物体の内部エネルギーの変化 、$Q$ が物体に加えた熱エネルギー、$W$ が物体にした仕事です。
熱力学では、熱エネルギーの受け渡し $Q$ と熱以外のエネルギーの受け渡し $W$ を区別して考えます。 熱以外のエネルギーの受け渡しを仕事と呼び、熱エネルギーの受け渡しは仕事と呼びません。 なぜわざわざ区別しなければならないのか。 それは次の熱力学第2法則でそれぞれの扱いがまったく異なるからです。
エネルギーは全体として増えもしないし減りもしないはず。 しかし我々はエネルギーを使い続ければやがて尽きてしまうこをと知っています。 このからくりはカルノーの発見「熱から動力を生み出すのには温度差が必要」なことにあります。 熱エネルギーは完全にリサイクルできるわけではないのです。
ウィリアム・トムソンは熱と仕事の関係についてこう述べました。
・熱をすべて仕事に変えることはできない
クラウジウスは熱の特殊性について次のような内容を述べました。
・熱が低温の物体から高温の物体に自然に流れることはない
・他に何の影響も残さず、低温の場所から高温の場所に熱を移すことはできない
これが熱力学第2法則です。
温度差のあるものを放っておけばそのうち温度差は埋まってしまいます。 グラスの中の氷も溶けてしまいます。 溶けてしまった氷も製氷機を使えば元に戻すことはできますが、 しかし我々はこれを何の資源も使わずに繰り返すことは不可能だと経験的に知っているはずです。
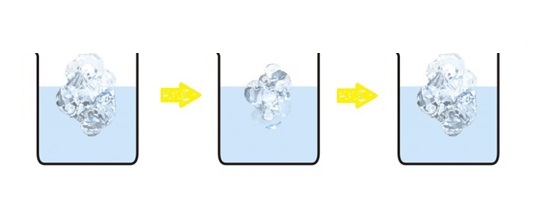
グラスの中で溶けてしまった氷を元に戻したとしても、この世界のどこかでエネルギーとは違う何かが失われているはずです。 この世界にある何をどうしようとも取り返しがつかない量。 それを説明するのがエントロピーです。
水も空気も生物も建築物も夜空の星々もすべての物はエントロピーという量を持っています。 これは内部エネルギーのように、物体の状態に応じて変化する量です。 しかし内部エネルギーよりもさらにイメージしにくい概念です。
物体に熱を加えればエントロピーは増え、物体から熱を奪えばエントロピーは減ります。 要するに熱エネルギーのようなものなのかというとそれもまた違います。 確かに熱エネルギーが多い方がエントロピーも高くなる傾向はあるのですが根本的にはまったく別のものです。
物体の温度が低い状態で熱を加えるとエントロピーは大きく増えてしまい、 物体の温度が高い状態で熱を奪ってもエントロピーはあまり減らないという特徴があります。 それだけでなく、エネルギーがまったく変わらなくてもエントロピーは増えることがあります。 例えばグラスに水と角砂糖を入れておけば混ざって砂糖水になりますが、 これが自然に水と角砂糖に戻ることはありません。 このときグラスの中のエントロピーは増えてしまったと考えられます。
物体がどのような状態のときどれだけエントロピーを持っているのか正確に知ることは難しいです。 簡単に測定して確かめられるものではないのですが、エントロピーの変化には次の法則が成り立つようなのです。
$ΔS$ が物体のエントロピーの変化 、$Q$ が物体に加えた熱エネルギー、$T$ が物体の温度です。
一旦エントロピーが増えてしまった物体を元の状態に戻そうとすれば、 その過程で必ず余分な熱が残ってしまいます。 その熱をどこかに捨てなければ元には戻らないのです。 しかしその熱を受け取った相手のエントロピーは必ずそれ以上に増えてしまうでしょう。 周囲になんの影響も与えずに覆水を盆に返すことはできないのです。
何のエネルギーも受け取らずに仕事をし続けることができる装置を第1種永久機関と呼びます。 これは熱力学第1法則(エネルギー保存則)から絶対にあり得ない存在です。 装置が仕事をすればそのぶん内部エネルギーが減り、いつかはエネルギーが尽きてしまうはずだからです。 いかなる装置も、外部からエネルギーを受け取らないで永久に仕事をし続けることはできません。
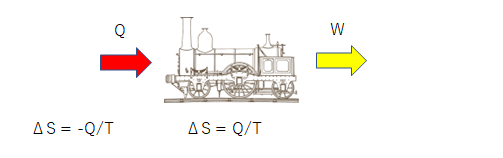
では次のように熱エネルギーをすべて仕事に変えて動き続ける装置を作ることができるでしょうか。 これは第2種永久機関と呼びますが、これも熱力学第2法則(エントロピーの法則)によって否定されています。
装置が外部から熱を受け取る一方で排出しなければ、装置のエントロピーが増えてすぐに上限に達してしまうことでしょう。 装置の温度は外気と差がなくなり最終的には熱を受け入れることができなくなります。 そうなればもうこの装置から仕事を取り出すことはできません。
装置を動かし続けるには、装置自身のエントロピーを上げないようにしなくてはなりません。 次の図のように装置の熱を外部に捨てる必要があります。 そして装置と外界をひとまとめに考えた場合にもエントロピーの法則が成り立っていなくてはなりません。 全体のエントロピーが減るような変化は起こり得ないはずです。 そして入ってくるエネルギーと出ていくエネルギーの収支も合っていなくてはなりません。
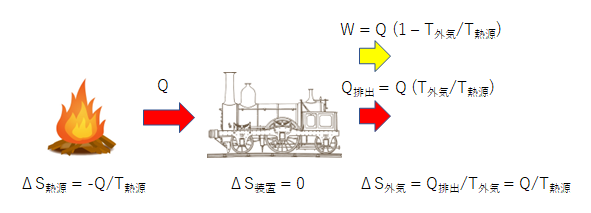
これらすべての辻褄を合わせるとこれ以上に効率のよい装置はどうやっても作れないはずです。 カルノーは蒸気機関から取り出せる最大の熱効率は $\displaystyle 1 - T_2/T_1$ と述べました。 エントロピーの観点からもそれは正しかったといえます。
熱は低温の物体から高温の物体に自然に流れないこともエントロピーの観点から説明できます。 低温の場所から高温の場所に熱を移動させようとすれば、取り込む熱より排出する熱の方が大きくなるはずです。 足りない分の仕事を外から与えてやらない限り熱が逆方向へ勝手に移動することはありません。
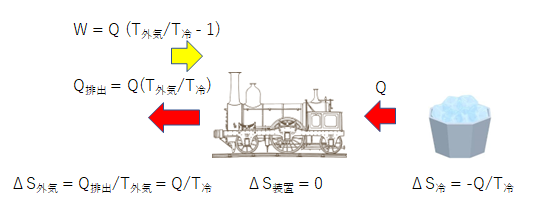
熱の出入りがない系では $ΔS ≧ 0$ となり、エントロピーが減ることはありません。 熱の出入りがないクーラーボックスの中ではエントロピーは増え続けることでしょう。 これを宇宙全体で考えてみれば宇宙全体でもエントロピー増大の法則は成り立つはずです。
この宇宙の中で、割れてしまったお皿、燃やしてしまった薪、溶けてしまった角砂糖、しぼんでしまった風船、腐ってしまった食材。 これらを放っておいて自然に元に戻ることはありません。 これらの変化が起こった後の宇宙は、変化が起こる前の宇宙よりエントロピーが高いと考えられます。 宇宙全体のエントロピーが増え続ければ、最終的にはエントロピーがそれ以上増えようがない状に落ち着くはずです。 これはどういう状態なのでしょうか。
すべての星は資源を使い果たし燃え尽きた状態です。 宇宙の温度は均一で、もはや熱を仕事に変えることができなくなっています。 生命も活動できない無機質な世界です。 このような状態になった宇宙にはそれ以上の変化が起こる余地はなく、エントロピーがそれ以上増える余地はありません。
逆に言えば、エントロピーが増える余地がどこかにあればエネルギーを取り出すことができるということです。 エントロピー増大の法則とは、熱の出入りのない系ではエントロピーが増え続けるという法則に他なりません。 宇宙のエントロピーが上限に達するのは太陽が燃え尽きたもっとずっと後の話です。 身の回りでエントロピーが増え続けているという話ではないのです。